Fixing Boundary Violations: Applying Constrained
Optimization to the Truncated Regression Model
2.3 Type II Boundary Constraints
Type II constraints are related to the regression coefficient \beta, which is best
illustrated by the centered model
\begin{equation*}
{{y}_{i}}=\boldsymbol{x_{i}^{*}\beta},
\end{equation*}
where \boldsymbol{{x}^{*}} refers to the matrix of the independent variables \boldsymbol{x_{j}}, j=1,\ldots ,m, after being centered at the means {{\bar{x}}_{j}},
\begin{equation*} \boldsymbol{x^{*}}=\left( \begin{matrix} \vdots & \vdots & & \vdots \\ 1 & \left( {{x}_{1i}}-{{\bar{x}}_{1}} \right) & \cdots & \left( {{x}_{mi}}-{{\bar{x}}_{m}} \right)\\ \vdots & \vdots & & \vdots \end{matrix} \right). \end{equation*}
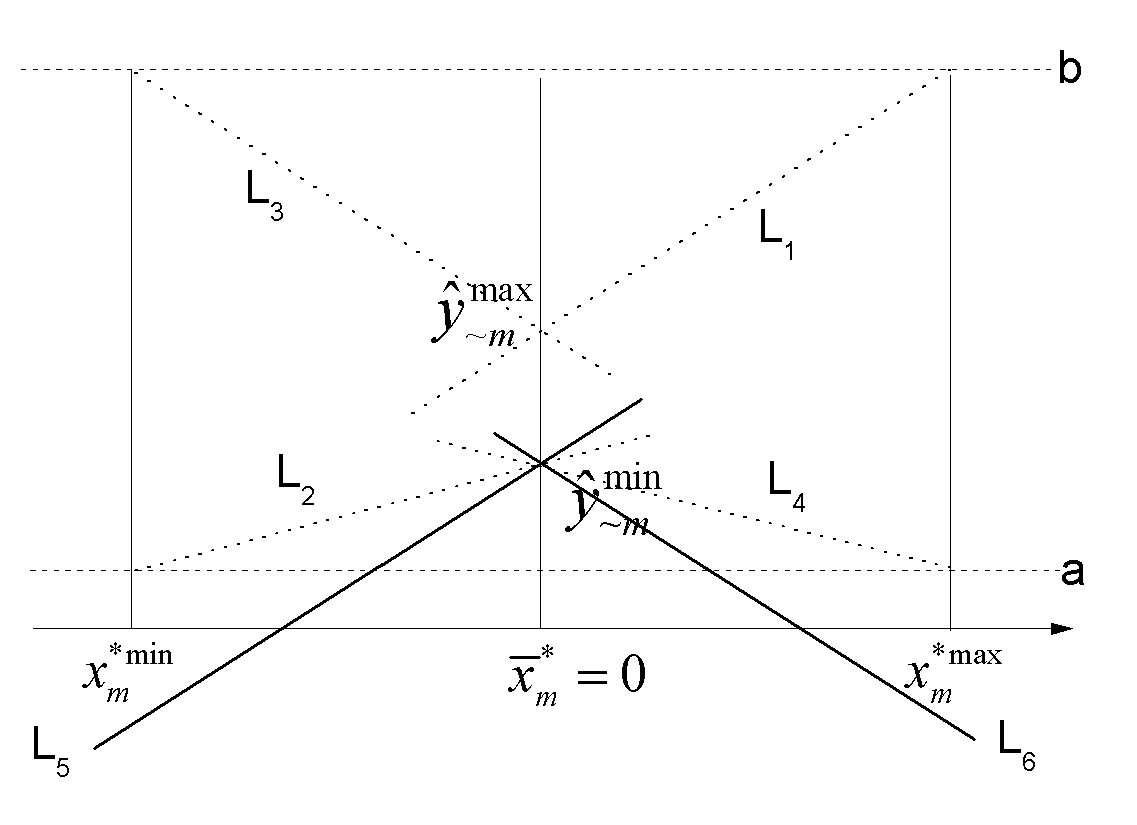
Figure 1 Boundary Constraints of \beta_{m}
The constant {{\hat{\beta }}_{0}} now represents the mean estimate of y_{i} when none
of the covariates has explanatory power, or represents the baseline predicted value of y_{i} when all covariates
are held by the means. Apparently, the boundary constraints of {{\hat{\beta }}_{0}} should be within the truncation
interval
\begin{equation*}
a\le {{\hat{\beta }}_{0}}\le b.
\end{equation*}
To discover the possible range of other {{\hat{\beta }}_{m}}, we first hold {{x}_{m}^{*}} at the mean level \bar{x}_{m}^{*} as Figure 1 shows, and then derive the maximum and minimum of the predicted values, \hat{y}_{\sim m}^{\max } and \hat{y}_{\sim m}^{\min }, respectively. The notation "\simm" represents the fact that {{x}_{m}^{*}} has no contribution when it is held at the mean. More precisely, \hat{y}_{\sim m}^{\max } and \hat{y}_{\sim m}^{\min } can be specified
\begin{align*} &\hat{y}_{\sim m}^{\max}=\sum\limits_{j=0,j\ne m}{\left(v_{j}^{+} {{\hat{\beta}}_{j}}x_{j}^{*\max}+v_{j}^{-}{{\hat{\beta}}_{j}}x_{j}^{*\min} \right)} \\ &\hat{y}_{\sim m}^{\min}=\sum\limits_{j=0,j\ne m}{\left(v_{j}^{+}{{\hat{\beta}}_{j}}x_{j}^{*\min}+v_{j}^{-} {{\hat{\beta}}_{j}}x_{j}^{*\max} \right)}. \end{align*}
The upper limit of \beta_{m} is the flatter positive slope of the line L_{1} or L_{2}. The lower limit is the flatter negative slope of the line L_{3} or L_{4}. Therefore, the boundary constraints of {{\hat{\beta }}_{m}} can be identified as
\begin{equation*} \max \left( \frac{a-\hat{y}_{\sim m}^{\min }}{x_{m}^{*\max }},-\frac{\hat{y}_{\sim m}^{\max }-b} {x_{m}^{*\min }} \right)\le {{\hat{\beta }}_{m}}\le \min \left( \frac{b-\hat{y}_{\sim m}^{\max }} {x_{m}^{*\max }},-\frac{\hat{y}_{\sim m}^{\min }-a}{x_{m}^{*\min }} \right). \end{equation*}
If \hat{\beta}_{m} takes the steeper slope, such as L_{5} or L_{6} shows, it would generate an out-of-bounds predicted value when we vary {{x}_{m}^{*}} from the mean to the maximum or minimum, holding other variables at the baseline level. In this sense, a type II violation can always be translated into a type I violation.
Different centering methods do not generate different estimates of the beta coefficients, except the constant, which is a linear combination of all other beta coefficients and the centered covariate values.7 For a truncated regression model with m covariates, there will always be (2m+2) type II boundary constraints, including the constant.
____________________
Footnote
7 This rule only applies to a strict linear model. If truncated regression is specified with a nonlinear relationship, such as interaction, different centering methods will generate different results.
